Making classifier evaluation less confusing

A short guide through the metric jungle: ROC AUC, F1, log loss and more.

ROC AUC, accuracy, specificity, log loss, calibration, confusion matrix, Brier score — evaluation of ML classifiers has caused me lots of confusion (pun intended). This post gives an overview of the big groups of evaluation metrics.

When learning about ML classification for the first time, the world is simple: To evaluate a classification model, we simply count the frequency of correct predictions. This evaluation metric is called accuracy. If we stopped here, we could have a happily ever after. Unfortunately, accuracy is a bad metric when data is imbalanced, and even with balanced data, it is a very rough evaluation metric with a lack of nuance.

Moving beyond accuracy, we quickly discover a chaotic flea market of metrics, which I find (found? it’s better now.) quite confusing.

The confusion starts with imprecise language.

What’s a classifier anyway?

The typical classification setup: We have a dataset. We have labels, each of which can be either 0 or 1, representing one of two classes. For simplicity, we focus on binary classification. We train a model and call it a classifier.

But we actually didn’t train a classifier; we trained a model that outputs a score and combined it with a threshold of usually 0.50 to turn the score into a classification. At least most modern classifiers are actually scorers plus a threshold (method).

Classifier = Scorer + Threshold

My goal isn’t linguistic pedantry, though, but deconstructing a classifier helps us categorize evaluation metrics.

Now we can clean up the mess and put evaluation metrics into one of four different boxes. And on each box, we can put a little sticker telling us which building blocks it evaluates.

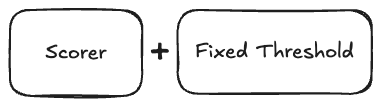
1) Classification metrics evaluate the classifier (scorer+threshold)

Classification evaluation metrics that are purely based on the predicted and actual classes evaluate the entire classifier, which means with a fixed threshold or threshold mechanism like majority vote. I’m talking about metrics like accuracy, sensitivity, specificity, F1, recall, and many more. They all can be derived from the confusion matrix, which counts pairs of predicted and actual classes.

Classification metrics evaluate the entire classifier

Classification metrics are particularly useful when your model will be used to make decisions. Because in this case, you have to pick a threshold (mechanism), and the classification metrics can tell you what kind of mistakes the classifier makes.

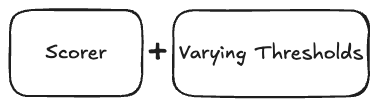
2) Sweeping-threshold metrics evaluate the scorer in combination with various thresholds

There’s a whole bunch of metrics that evaluate the scorer and a range of different thresholds, and unite them in one plot or number. The typical example is the ROC curve, which plots true positive rate against false positive rate and can be turned into a metric by measuring the area underneath, with the beautiful name of ROC AUC.

Sweeping-threshold metrics evaluate the scorer in combination with many thresholds

By sweeping through many thresholds, these evaluation metrics become agnostic of any particular threshold, but still summarize performance across thresholds.

3) Scoring rules evaluate probabilistic scorers

Scoring rules like the log loss or the Brier score work directly on probabilistic scorers, which output numbers between 0 and 1. Scoring rules measure how much the predicted score is aligned with the correct class and are independent of any type of threshold. The larger the probability for the correct class, the better the score (typically means a smaller log loss or Brier score).

Scoring rules evaluate probabilistic scorers

Scoring rules overlap with loss functions that are used to train the models (e.g., the log loss for a neural network). If you have two models that spit out exactly the same classifications, they will have the same classification metrics (F1, precision, …). Their, for example, log loss, however, will still be different if one model is more confident in the correct predictions. Scoring rules are insufficient for judging the actual decision performance of a model, because this also depends on the decision mechanism.

4) Calibration metrics evaluate probabilistic scorers

Calibration plots and metrics check whether the model predictions of a probabilistic classifier reflect the frequencies in the data distribution. For example, images where a model predicts a 90% probability of showing a dog, then among these images, we’d expect ~90% to be truly dogs.

Calibration metrics evaluate probabilistic scorers

However, calibration is kind of independent of the other metrics. For example, you can create a perfectly calibrated model for predicting a coin toss, but it won’t be able to actually predict the coin toss better than random chance. So calibration isn’t a standalone evaluation metric, but an auxiliary one.

If you liked that kind of birds-eye view on machine learning, I’m writing a book that may be of interest to you. The current working title is Elements of ML Algorithms, but now I’m considering naming it “Building Blocks of Machine Learning”. You can sign up for updates here: