Why SHAP needs to be estimated
Exploring the Necessity of Estimation in Machine Learning Interpretation
SHAP is an explanation technique used to explain predictions of machine learning models. SHAP values can’t be calculated exactly, but instead, have to be estimated.
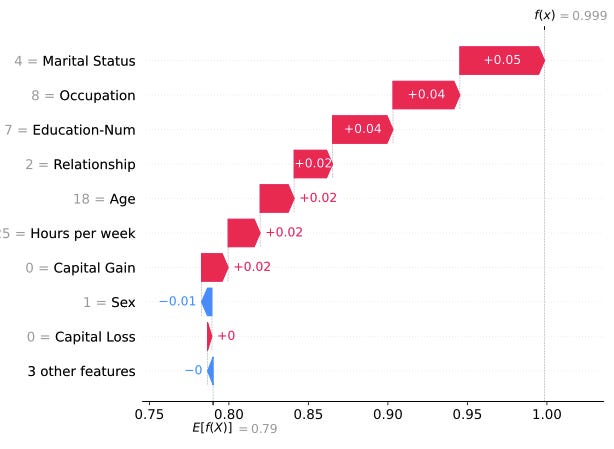
If you don’t know SHAP you still might have encountered plots like the following, which attributes a model prediction (probability of earning more than $50k) to the individual features such as marital status and occupation.
SHAP is based on Shapley values, a concept from game theory. The setting: A team of players collaborates to get some payout which they want to fairly divide among each other. Players might have contributed differently, so some should get more, and others should get less.
The original Shapley values can be calculated exactly at least for simple games. Without going into details, the calculation of the contribution of a single player works by
enumerating all possible team coalitions
measuring the payout for each coalition with and without the player of interest
averaging the differences, weighted by a factor based on coalition size
Why can’t we do the same for SHAP explanations in machine learning?
SHAP values have to be estimated
The idea behind SHAP values: the prediction is the payout of a game, and the feature values of a data point work together as a team to get that payout. We fairly distribute the payout among these “team players”. The payout for each feature is called SHAP value.
There are two reasons why we have to rely on estimation for SHAP values.
Reason #1: Too many features, too many coalitions
Theoretical Shapley values are defined by iterating all possible coalitions. This number of coalitions scales exponentially with the number of players: 2^p.
In machine learning, it’s often the case that you have many features. 100 features wouldn’t be unusual. Some people might even laugh at this number because they have thousands of features or more.
The good thing is: We don’t have to compute all coalitions, but we can sample from them. But that also means that the resulting SHAP values become estimates of the Shapley values and are no longer exact.
But even if you can compute all coalitions, for example, when you have 10 features or fewer, the resulting SHAP values will still be estimates.
Reason #2: Working with distributions
How do we get the payout of an arbitrary coalition of features? Let’s say you have a classification model for disease diagnosis. To get the SHAP value of, say, the red blood cell count, you add them to arbitrary coalitions of features. But how do you get the prediction for just some of the features with other features missing? Most models can’t handle missing data by default.
The trick of SHAP is to integrate the prediction function with respect to the distributions of the absent features. But this comes with a problem: We don’t know the distribution. Even if we knew the distributions, we wouldn’t get a closed form of the integral of the prediction function with respect to the distributions.
But we do have data and can utilize Monte Carlo integration. Instead of integrating the function, we randomly draw other data instances and replace the absent features with these sampled values and average the prediction over those samples. Through Monte Carlo integration we get an estimate of the integral.
I dive deeper into the estimation and application of SHAP values in my coming book Interpreting Machine Learning Models With SHAP: A Comprehensive Guide With Python. The planned release date is the 1st of August. You can sign up here to get notified when the book is released along with an early bird coupon: