Week #1: Getting Started With Conformal Prediction For Classification
Using conformal prediction in just 3 lines of code
Reading time: 10 min
Check out my book on Conformal Prediction which provides hands-on examples to quantify uncertainty in your application!
Welcome to course week #1 of Introduction to Conformal Prediction.
The course is designed to be short and lightweight, with a list of resources for those who want to dive deeper.
I’m learning together with you, so if something is unclear, please leave a comment, and be kind if I make mistakes 😅.
This week you will learn
not to trust uncalibrated uncertainty scores
the basic idea of conformal prediction
how to apply conformal prediction to multi-class classification
Don’t Trust Model Predictions
Machine learning predictions are like best guesses of the true outcome. A guess can be on point but sometimes it’s just a wild guess.
Without uncertainty quantification, accurate predictions and wild guesses look the same.
Getting only a point prediction of unknown certainty can be problematic:
Decisions based on predictions should take uncertainty into account. It matters if forecasted product demand has a prediction interval of [99, 101] or [50, 120].
An ML product that shows wrong predictions with high confidence to the user is not trustworthy.
Using machine learning to automate things? Maybe some cases need human intervention and uncertainty quantification can help to select the uncertain ones.
Good news: We have many approaches to quantify uncertainty, from Bayesian predictive intervals to variance in model ensembles. Especially multi-class classification seems “solved” since models like the random forest output “probabilities” which could be interpreted as uncertainty scores.
Unfortunately, we shouldn’t interpret these scores as actual probabilities — they just look like probabilities but are usually not calibrated. Probability scores are calibrated if, for example, among all classifications with a score of 90% we find the true class 9 out of 10 times.
Same problem for all other approaches: They are either uncalibrated or rely on strong distributional assumptions like priors and Gaussians to be correct.
The naive approach: take at face value the uncertainty scores that the model spits out - confidence intervals, variance, Bayesian posteriors, multi-class probabilities.
At first glance, conformal prediction seems like yet another approach to uncertainty quantification. But conformal prediction is a versatile method that can turn any other uncertainty method into a trustworthy tool.
What Is Conformal Prediction?
Conformal prediction is a method that takes an uncertainty score and turns it into a rigorous score. “Rigorous” means that the output has probabilistic guarantees of covering the true outcome.
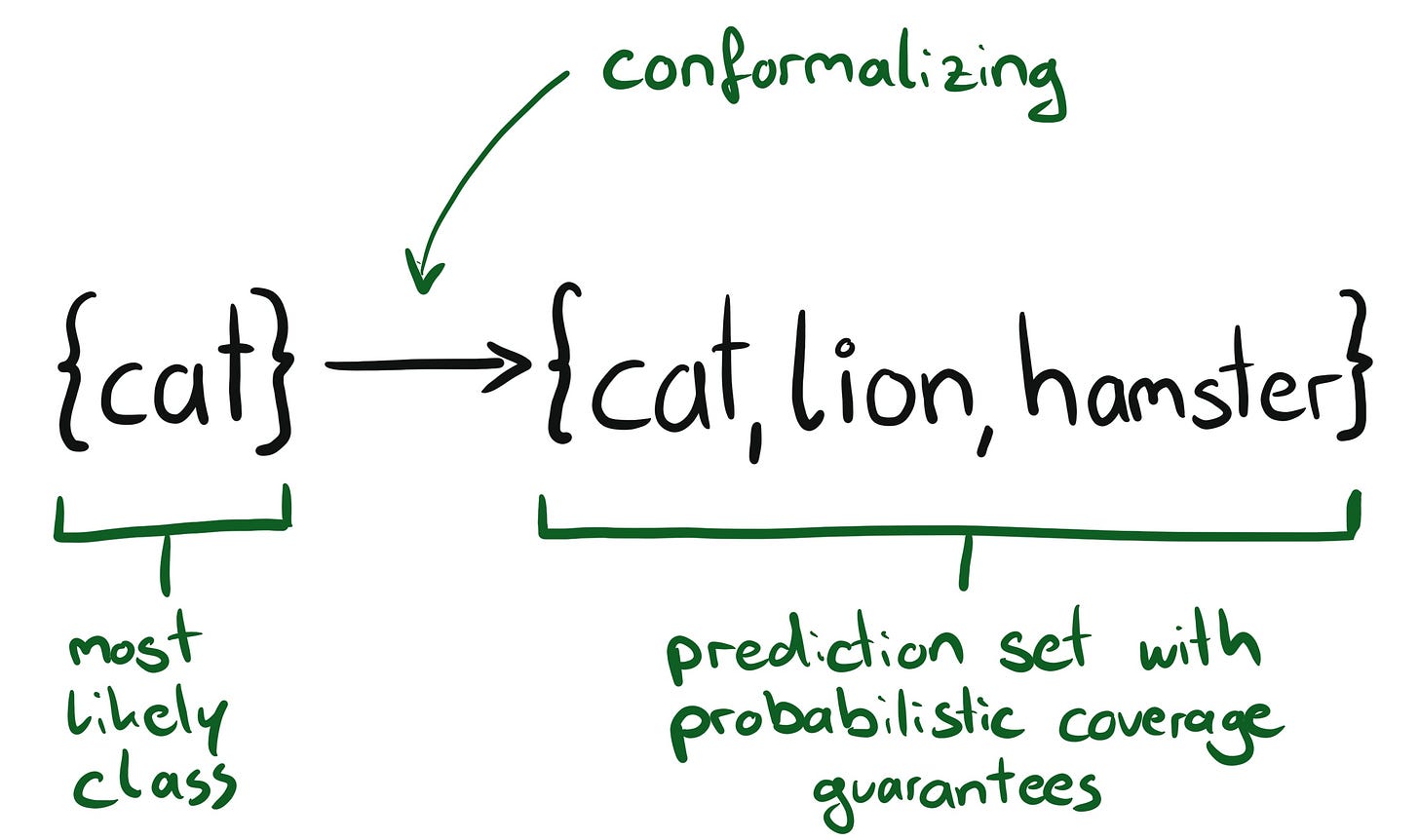
Conformal prediction changes what a prediction looks like: it turns point predictions into prediction sets. For multi-class classification it turns the class output into a set of classes:
Conformal prediction has many advantages that make it a valuable tool to wield:
distribution-free: the only assumption is that data points are exchangeable.
model-agnostic: conformal prediction can be applied to any predictive model.
coverage guarantee: the resulting prediction sets come with guarantees of covering the true outcome with a certain probability.
And it’s super simple to apply. Just 3 lines of code. You will see.
Classifying Beans
Let’s jump right into an example: Classifying dry beans.
A (fictive) bean company uses machine learning to automatically classify beans into 1 of 7 different varieties: Barbunya, Bombay, Cali, Dermason, Horoz, Seker, and Sira.
The bean dataset contains around 13k beans (Koklu and Ozkan 2020). Each row is a dry bean with 8 measurements such as length, roundness, and solidity, in addition to variety, the prediction target.
The bean varieties have different properties, so it makes sense to classify them and sell the beans by variety. Automating this task with machine learning frees up a lot of time as the job would have to be done manually otherwise.
The model was trained in ancient times by some legendary dude that has long left the company. It’s a Naive Bayes model. And it sucks.
model = GaussianNB().fit(X_train, y_train)Model accuracy is 76%.
Unfortunately, the model can’t be easily swapped out because it’s hopelessly entangled with the rest of the backend at the beans company. And nobody wants to be the one who pulls the wrong piece out of this Jenga tower of a backend
The dry bean company is in trouble. Multiple customers complained that they bought bags of one type of variety but there were too many beans of other varieties mixed in.
The bean company holds an emergency meeting and it’s decided that they will offer premium products with a guaranteed percentage for the advertised bean variety. For example, a bag labeled “Seker” should have at least 95% Seker beans.
Naive Approach To Uncertainty
Great, now all the pressure is on the data scientist to provide such guarantees all based on that bad model. Her first approach is the “naive approach” to uncertainty which means taking the probability outputs and believing in them.
So instead of just using the class, she takes the predicted probability score, and if that score exceeds 95%, the bean makes it into the 95%-bag.
It’s not yet clear what to do with beans that don’t make the cut for any of the classes but stew seems to be the most favored option among the coworkers.
The data scientist doesn’t fully trust the model scores, so she checks the coverage of the naive approach. Luckily she has access to new, labeled data that she can use to estimate how well her approach works.
She 1) gets the probability predictions for the new data, 2) keeps only beans with >=0.95 predicted probability, and 3) checks how often the ground truth is actually in that 95%-bag.
Ideally, 95% or more of the beans should have the predicted class, but she finds that the 95%-bag only contains 89% of the correct variety.
What now?
She could use methods such as Platt scaling or isotonic regression to calibrate those probabilities, but again, without guarantees of correct coverage for new data.
But she has an idea.
Start With The Guarantee
The data scientist decides to think differently about this problem: Don’t start with the probability scores, but start thinking about how she can achieve a 95% coverage guarantee.
Can she produce a set of predictions for every bean that covers the true class with 95% probability? Seems to be a matter of finding the right threshold.
So she does the following:
She ignores that the output could be a probability. Instead, she uses the model “probabilities” to construct a measure of uncertainty:
s_i = 1 - f(x_i)[y_i].
A bit sloppy notation for saying that we take 1 minus the model score for the true class (if the ground truth for bean number 8 is “Seker” and the probability score for Seker is 0.9, then s_8 = 0.1).
Then she does the following to find the threshold:
start with fresh data
compute the scores
s_isort the scores from low (certain) to high (uncertain), see the figure below
compute the threshold
qwhere 95% of thes_i’s are lower (=95% quantile)
This is what the distribution of scores looks like, from left (certain) to right (uncertain). The threshold should be chosen so that 95% of the true bean classes are covered.
In this case, the threshold is 0.999.
How is that threshold useful? We know that for bean uncertainties s_i below 0.999 (equivalent to class “probabilities” > 0.001) we can be sure that with a probability of 95% we have the correct class included.
But there’s a catch: For some data points, there will be more than one class that makes the cut. But sets are not a bug, they are a feature of conformal prediction.
And that’s it. You just witnessed conformal prediction in action.
DIY Conformal Prediction For Classification
Yep, it can be this simple. In Python, this version of conformal prediction is just 3 lines of code:
predictions = model.predict_proba(X_calib)
prob_true_class = predictions[np.arange(len(y_calib)),y_calib]
qhat = np.quantile(1 - prob_true_class, 0.95) With a small correction: For conformal prediction, the data scientist shouldn’t use a 0.95 quantile, but instead, apply a finite sample correction, i.e. multiplying 0.95 with (n+1)/n which is 0.951 for n = 1000.
An important part of conformal prediction is that the data (X_calib, y_calib) used for finding that threshold is not used for training the model.
For new data points the data scientist can turn the prediction into prediction sets by using the threshold:
prediction_sets = (1 - model.predict_proba(X_new) <= qhat) Let’s have a look at the predictions sets for 3 “new” beans (X_new):
['BOMBAY'], ['BARBUNYA' 'CALI'], ['SEKER' 'SIRA'].
On average, the prediction sets have the probability to cover the true class with a probability of 95%. The first set only has 1 bean variety “Bombay”, so we would package it into a Bombay set.
Beans #2 and #3 have prediction sets with two varieties each. Maybe a chance to offer bean products with guaranteed coverage, but which contain two varieties? Everything with more categories could be sorted manually or the CEO could finally make bean stew for everyone.
The CEO is relaxed now and more confident in the product.
Spoiler alert: the guarantees don’t work the way the bean CEO believes, as we will soon learn.
Conformal Prediction With MAPIE
The data scientist could also have used MAPIE, a Python library for conformal prediction.
from mapie.classification import MapieClassifier
cp = MapieClassifier(estimator=model, cv="prefit", method="score")
cp.fit(X_calib, y_calib)
y_pred, y_set = cp.predict(X_new, alpha=0.05)If you are familiar with sklearn, you will feel at home with MAPIE as the library follows the sklearn API with .fit() and .predict()methods.
MAPIE implements many different conformal predictors and you will meet this library again in this course.
Understanding Coverage
The bean CEO celebrated too early.
The data scientist found out that the coverage guarantee only holds on average across all data points, also called “marginal” coverage. There is currently no guarantee that the coverage holds for each variety.
Coverage = percentage of prediction sets that contain the true label
So the data scientist checks coverage (cov) and average set size by variety on all the new data points (n=1000) that weren’t used for training or calibrating the model.
The “Bombay” variety has 100% coverage with only sets of size 1. The worst coverage is for the variety “Sira” with a coverage of only 92.2%. The bean CEO can relax a bit since the coverages are not too far off. But still, the data scientist has to put more work in.
Adaptive Prediction Sets
The problem is that the current conformal predictor is not adaptive to the difficulty of the classification, but the desire is to have conditional coverage.
While conformal predictors always guarantee marginal coverage, conditional coverage is not guaranteed. Adaptive conformal predictors approximate conditional coverage.
You might have already spotted a different way to construct a score: Add up all the probabilities, starting with the highest one, until we reach the true class. This algorithm is called “Adaptive Prediction Sets”.
It’s not too complicated to implement APS in Python, but it’s even easier to do it in MAPIE. Just change the method within the MapieClassifier:
cp = MapieClassifier(model, cv="prefit", method="cumulated_score")There are even more methods for conformalizing classifiers, but that would go too far at this point. Check out the further resources for more information.
That’s a wrap for this week! Next week we will explore the intuition behind conformal prediction and learn how conformal prediction is a framework, not just a single method.
Further Resources
Are you motivated to dive deeper into conformal prediction for classification? Here are some further pointers:
Checkout the different conformal classification methods implemented in MAPIE
Read chapters 1 and 2.1 of the paper A Gentle Introduction to Conformal Prediction
Scroll through the Awesome Conformal Prediction list. It’s like the superstore for conformal prediction where you will find everything, but it can be overwhelming on your first visit.
If you have any questions, don’t hesitate to comment on substack. I will try to answer to the best of my knowledge. Keep in mind that I’m also just getting started with conformal prediction.
I know that some of the top experts on conformal prediction subscribed to the course as well, so hopefully, they can help out with difficult questions 😇
If you think someone might enjoy the course, please forward them this newsletter.
If you haven’t subscribed yet, subscribe here and automatically get the next course e-mails:









Thanks a lot for this course! Love the intuitive step-by-step explanation and the hands-on example (eg choosing a concrete dataset like the Beans dataset is great).
A little question about the procedure though. Say you take the frequency plot (which contains the predicted probas for all predictions, across all different classes). We applied the 0.999 threshold such that 95% of the data points include the true class. Now, 95% was chosen arbitrarily. Let’s say someone has the idea to just set the threshold to 1.0 to get 100% coverage. Or in other words with that procedure someone can always achieve 100% coverage by setting the threshold to 1.0, which sounds good on paper but is not actually doing anything useful. Maybe I am misunderstanding something but would you mind clarifying?
Excellent introduction on CP. Looking forwards to read more blogposts on it. Unfortunately 'conformal prediction' approach of evaluating uncertainty has been 'missing ' in popular machine learning books and tutorials although there are plenty of academic articles have been published last few years.